Autotutor Maths Practice High School Exams. Pythagoras Theorem Proof.

This website will not work correctly if Javascript is disabled.

Email address:
Password:

Pythagoras Theorem Proof

Step 1.

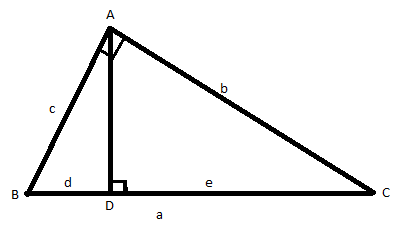
Draw triangle ABC. Draw perpendicular AD from A to BC. Let a = BC, b = AC, c = AB, d = BD, and e = DC. Note that a = d + e .

Step 2.

Note that the three triangles are similar.

ABC is similar to DBA because each has a right angle, and angle ABD is common to each triangle. This meets the similarity condition (AA) of two angles being the same.

By the same argument ABC is similar to DAC.

Therefore: the three triangles are similar. (The order of the triangle corners is significant.)

Step 3.

For each small triangle compared to the large triangle note the ratios of the corresponding sides using (for the small triangle) the hypotenuse and the side along BC.

So: in DBA and ABC as these are similar: c/a = d/c

So: c² = ad (1)

Similarly, in DAC and ABC: b/a = e/b

So: b² = ae (2)

Step 4.

Adding (1) and (2) gives: b² + c² = ad + ae = a (d + e) = a²

This is the required result.